mydf <- readr::read_csv("~/mmedr/breastcancer.csv") |>
janitor::clean_names()Statistical tests
In this section, we will cover basic statistical tests to conduct hypothesis testing for different combinations of continuous, categorical, and paired data.
You will need to load the breast cancer data for use in this section. Clean the names using the clean_names() function from the {janitor} package, and save it as object mydf.
Two categorical variables
There are two main tests for associations between two categorical variables: the chi-squared test and Fisher’s exact test.
Conduct these tests in R using the following functions:
chisq.test()fisher.test()
Conduct a chi-squared test of the null hypothesis that there is no association between grade and radiation therapy versus the alternative hypothesis that there is an association between grade and radiation therapy.
chisq.test(x = mydf$grade, y = mydf$rt)
Pearson's Chi-squared test
data: mydf$grade and mydf$rt
X-squared = 34.948, df = 2, p-value = 2.577e-08The chi-squared test statistic is 34.948 with associated p-value 2.5765086^{-8}.
Reject the null hypothesis since the p-value is less than the traditional threshold for significance of 0.05.
Note, we could report this p-value as p<0.001, or to journal requirements
Conduct a Fisher’s exact test (an alternative to the chi-squared test when any expected cell count is <5):
fisher.test(x = mydf$grade, y = mydf$rt)
Fisher's Exact Test for Count Data
data: mydf$grade and mydf$rt
p-value = 2.734e-08
alternative hypothesis: two.sidedThe p-value is 2.7343786^{-8}.
Reject the null hypothesis since the p-value is less than the traditional threshold for significance of 0.05.
One continuous, one categorical
The most common statistical tests for the association between a continuous and a categorical variable are the non-parametric Kruskal-Wallis test and the parametric t-test.
Conduct these tests in R using the following functions:
kruskal.test()(see alsowilcox.test())t.test()
Note that the Kruskal-Wallis test is also known as the Wilcoxon rank-sum test in the special case of a 2-level categorical variable.
“Non-parametric” means that there is no parametric distribution assumption made on the continuous variable - i.e. the continuous variable is not assumed to be normally distributed.
Conduct a Kruskal-Wallis test to test the null hypothesis of no association between age and radiation therapy versus the alternative hypothesis that there is an association between age and radiation therapy.
kruskal.test(age_dx_yrs ~ rt, data = mydf)
Kruskal-Wallis rank sum test
data: age_dx_yrs by rt
Kruskal-Wallis chi-squared = 104.18, df = 1, p-value < 2.2e-16Since “response” is a 2-level categorical variable, the Wilcoxon rank-sum test (without continuity correction) produces the same result:
wilcox.test(age_dx_yrs ~ rt, correct = FALSE, data = mydf)
Wilcoxon rank sum test
data: age_dx_yrs by rt
W = 1326112, p-value < 2.2e-16
alternative hypothesis: true location shift is not equal to 0With a p-value of 1.8469697^{-24}, reject the null hypothesis at the 0.05 significance level.
“Parametric” means that the test assumes a parametric distribution - in the case of the t-test, it relies on the assumption that the continuous variable is normally distributed.
If appropriate given the distribution of the continuous variable, conduct a t-test:
t.test(age_dx_yrs ~ rt, data = mydf)
Welch Two Sample t-test
data: age_dx_yrs by rt
t = 10.667, df = 2608.5, p-value < 2.2e-16
alternative hypothesis: true difference in means between group 0 and group 1 is not equal to 0
95 percent confidence interval:
4.409767 6.396293
sample estimates:
mean in group 0 mean in group 1
60.48659 55.08356 The conclusion is the same: reject the null hypothesis that there is no association between marker and response.
And we can visually confirm that age is approximately normally distributed, so that this test is appropriate:
library(ggplot2)
ggplot(data = mydf, aes(x = age_dx_yrs)) +
geom_histogram(bins = 10)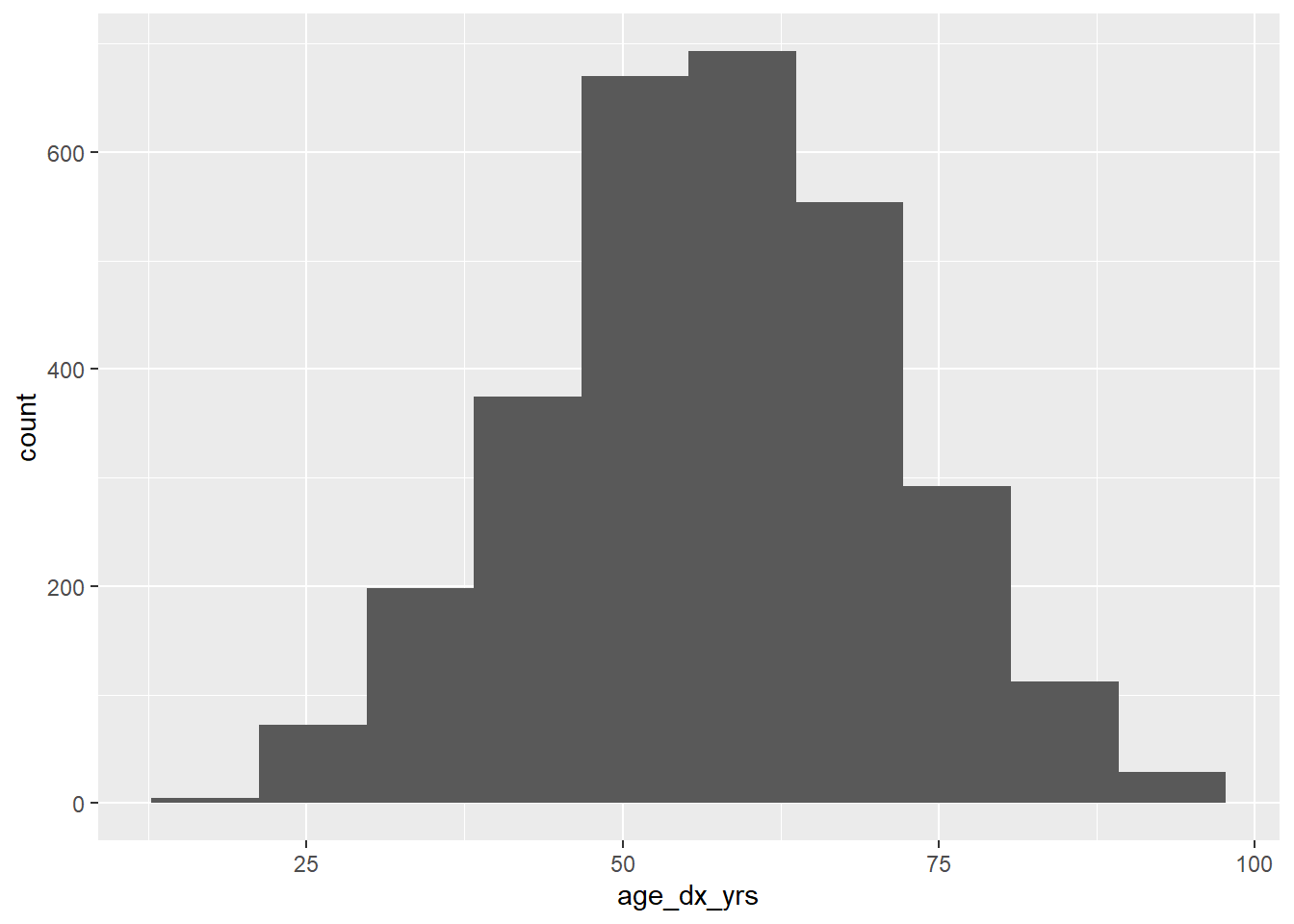
Tips:
- For the preceding two tests we used the
formulaoption to supply the information for the test - A formula in R looks like
LHS ~ RHSwhere the left-hand side (“LHS”) is typically an outcome variable or dependent variable and the right-hand side (“RHS”) is the independent variable. - For multivariable regression, you can specify formulas in the format
Y ~ X1 + X2 + X3...when there is more than one independent variable. - Using the formula option, you must also supply the name of the dataset to the
data =argument so that R knows where to look to find the specified variables. - See the help files for alternative ways to supply the information for each test
What if our categorical variables has more than 2 levels, but we want to do a parametric test? Then we will use ANOVA. ANOVA tests the null hypothesis of no association between marker and grade, which has more than two levels so a t-test is not appropriate, and relies on the assumption that the continuous variable is normally distributed.
lm_mod <- lm(age_dx_yrs ~ grade, data = mydf)
anova(lm_mod)Analysis of Variance Table
Response: age_dx_yrs
Df Sum Sq Mean Sq F value Pr(>F)
grade 2 760 380.16 1.9823 0.1379
Residuals 2997 574764 191.78 And here we would not reject the null hypothesis of no association between age and grade, at the 0.05 level, since the resulting p-value is 0.1379383, which is >0.05.
Note that sometimes it can be hard to figure out how to extract the p-value from test results. Here are two tips.
First, assign your model results to an object, and examine in one of two ways.
temp <- t.test(age_dx_yrs ~ rt, data = mydf)Then use str() to look at the structure:
str(temp)List of 10
$ statistic : Named num 10.7
..- attr(*, "names")= chr "t"
$ parameter : Named num 2608
..- attr(*, "names")= chr "df"
$ p.value : num 4.98e-26
$ conf.int : num [1:2] 4.41 6.4
..- attr(*, "conf.level")= num 0.95
$ estimate : Named num [1:2] 60.5 55.1
..- attr(*, "names")= chr [1:2] "mean in group 0" "mean in group 1"
$ null.value : Named num 0
..- attr(*, "names")= chr "difference in means between group 0 and group 1"
$ stderr : num 0.507
$ alternative: chr "two.sided"
$ method : chr "Welch Two Sample t-test"
$ data.name : chr "age_dx_yrs by rt"
- attr(*, "class")= chr "htest"Alternatively, open the object by clicking on it in the Environment tab. Then hover over the item you want to return, and you can get the code to extract it.
Paired data
Next we consider the setting where we have paired data. Paired data are any data where a continuous variable is matched in a meaningful way between the two groups. Examples:
- Pre vs post drug/surgery/test/etc on a single subject
- Measurements on two eyes within subject
- Sibling or spousal pairs
We will use the example data from the help page found by running ?wilcox.test. These are measurements of a continuous depression scale on 9 patients taken at the first (x) and second (y) visits after initiation of a certain therapy. We want to test the null hypothesis that there is no difference in depression scale values between these two times.
x <- c(1.83, 0.50, 1.62, 2.48, 1.68, 1.88, 1.55, 3.06, 1.30)
y <- c(0.878, 0.647, 0.598, 2.05, 1.06, 1.29, 1.06, 3.14, 1.29)The Wilcoxon signed-rank test is a non-parametric test for the association between paired continuous data. Note that this is the same function we used for the Wilcoxon rank-sum test previously, with non-paired data, only now we add the paired = TRUE argument.
wilcox.test(x, y, paired = TRUE)
Wilcoxon signed rank exact test
data: x and y
V = 40, p-value = 0.03906
alternative hypothesis: true location shift is not equal to 0We reject the null hypothesis at the 0.05 level.
For demonstration purposes we also try the paired t-test, which requires data to be normally distributed, to test the null hypothesis that there is no difference in depression scale values between these two times. Again, note that this is the same function we used for the standard t-test previously, only now we have added the paired = TRUE argument.
t.test(x, y, paired = TRUE)
Paired t-test
data: x and y
t = 3.0354, df = 8, p-value = 0.01618
alternative hypothesis: true mean difference is not equal to 0
95 percent confidence interval:
0.1037787 0.7599991
sample estimates:
mean difference
0.4318889 And again we reject the null hypothesis at the 0.05 level.